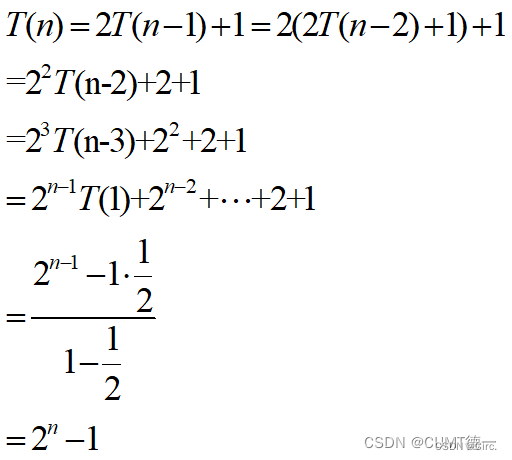递归与迭代

接上一篇 “函数练习-2” ，继续探讨函数递归问题。

上一篇我们了解了什么是递归，和递归的基本思想：把规模大的问题转化为规模小的相似的子问题来解决。

那么，什么是迭代呢？

迭代（iteration）：重复反馈过程的活动，每一次迭代的结果会作为下一次迭代的初始值。（A重复调用B）。（aka：重复执行一系列运算步骤，从前面的量依次求出后面的量的过程。此过程的每一次结果，都是由对 前一次所得结果 施行相同的运算步骤 得到的）

迭代不一定是循环，循环是迭代的一种方式。

练习3: 求n的阶乘。(不考虑溢出)

在“循环练习-1”中有讨论求n的阶乘的问题，在当时我们选择的是通过一个for循环来进行求解：

1
2
3
4
for (int i = 1; i <= n; i++)
{
	temp = temp * i;
}

那么我们有没有可能通过递归的思想来求解呢？

其实很简单，不考虑溢出（stack overflow）的情况下，很容易有以下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>

int Fac(int n)
{
    if (n <= 1)
        return 1;
    else
        return n * Fac(n - 1);
}

int main()
{
    int temp = 0;
    scanf("%d", &temp);
    printf("%d\n", Fac(temp));
    return 0;
}

判断n是否小于等于1，如果为真则返回1，如果不为真，则返回n*Fac(n-1)。

image-20240131100701491

为什么要用小于等于，而不是直接等于1呢，此时我们要考虑一种特殊情况就是0的阶乘也是1。（负数无法处理）

练习4: 求第n个斐波那契数。(不考虑溢出)

斐波那契数列1，1，2，3，5，8…，和卢卡斯数列1，3，4，7，11，18…，具有相同的性质：从第三项开始，每一项都等于前两项之和，我们称之为斐波那契—卢卡斯递推。凡符合斐波那契—卢卡斯递推的数列就称为斐波那契—卢卡斯数列。

别名有斐波那契—卢卡斯序列，推广斐波那契数列，推广卢卡斯数列，推广兔子数列等。

也就是说，后面一项都为前两项相加，那么如何求第n个斐波那契数呢？

我们可以通过数学的数列思想来拆分求斐波那契数的原理,假设定义Fib(n)函数求第n个斐波那契数：

当 n <= 2 ，1

当 n > 2 , Fib(n-1)+Fib(n-2)

那么是不是和练习3的思想非常相似呢，那么将代码做小小的修改就有：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>

int Fib(int n)
{
    if (n <= 2)
        return 1;
    else
        return Fib(n-1)+Fib(n-2);
}

int main()
{
    int n = 0;
    scanf("%d", &n);
    printf("%d\n", Fib(n));
    return 0;
}

image-20240131101840536

但是，当数字大一点的时候，计算的速度就会非常慢，所需的时间会很长，这是为什么呢？因为在递归中，我们进行了大量重复的计算，极大降低了效率。

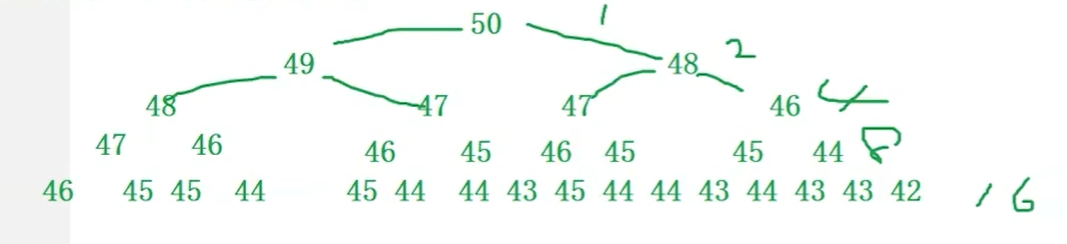
image-20240131102241433

假设需要求第50个斐波那契数，就需要知道49和48的斐波那契数，如果

想知道49和48的，又需要计算48、47和47、46的斐波那契数，以此类推，从1->2->4->8->16可以看出，所需计算次数呈2的n次方增长（爆炸式增长哈哈）。

那么这样的代码效率就非常低，但是我们发现上面有很多其实已经计算过了，是不是有大量重复的计算呢？

image-20240131103352220

由此不断迭代，是不是可以直接求出最后一个c的值直接返回，而不用重复计算呢？那么根据这个思想怎么写出代码呢？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>

int Fib(int n)
{
    int a = 1;
    int b = 1;
    int c = 1;
    while (n > 2)
    {
        c = a + b;
        a = b;
        b = c;
        n--;
    }
    return c;
}

int main()
{
    int n = 0;
    scanf("%d", &n);
    printf("%d\n", Fib(n));
    return 0;
}

通过迭代的思想，我们可以先设置三个变量a，b，c，初始化为1，这样当n小于2的时候，刚好返回c的值就是1。

当n大于2的时候，令c = a + b，再将b的值赋值给a，c的值赋值给b，用于下一次计算c = a + b。

由此大大降低了计算所需的次数，降低时间复杂度。

image-20240131103827943

结果一致。

代码可以用递归写，也可以不用递归写，如果递归的方式有明显的缺陷，即使比较容易实现，但我们也需要用非递归的方式进行求解来解决这个缺陷（可能是栈溢出，可能是效率低等等）。

递归经典问题：

1.汉诺塔问题

img

汉诺塔（Hanoi Tower）问题是一个经典的数学谜题和递归问题。它是基于一个传说而得名，传说中有一座位于印度寺庙的塔，塔内有三个柱子，其中一个柱子上摞着64个大小不同的圆盘，从底部开始呈递减的形式。目标是将这些圆盘按照规定的规则从初始柱子（通常是最左边的柱子）移动到目标柱子（通常是最右边的柱子），并且在整个过程中遵守以下规则：

1、每次只能移动一个圆盘。
2、不能将较大的圆盘放在较小的圆盘上。

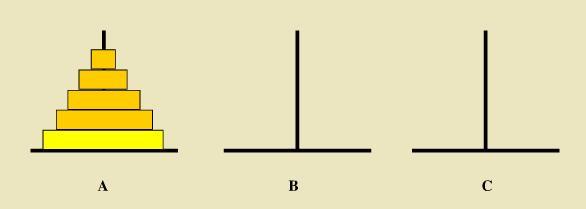
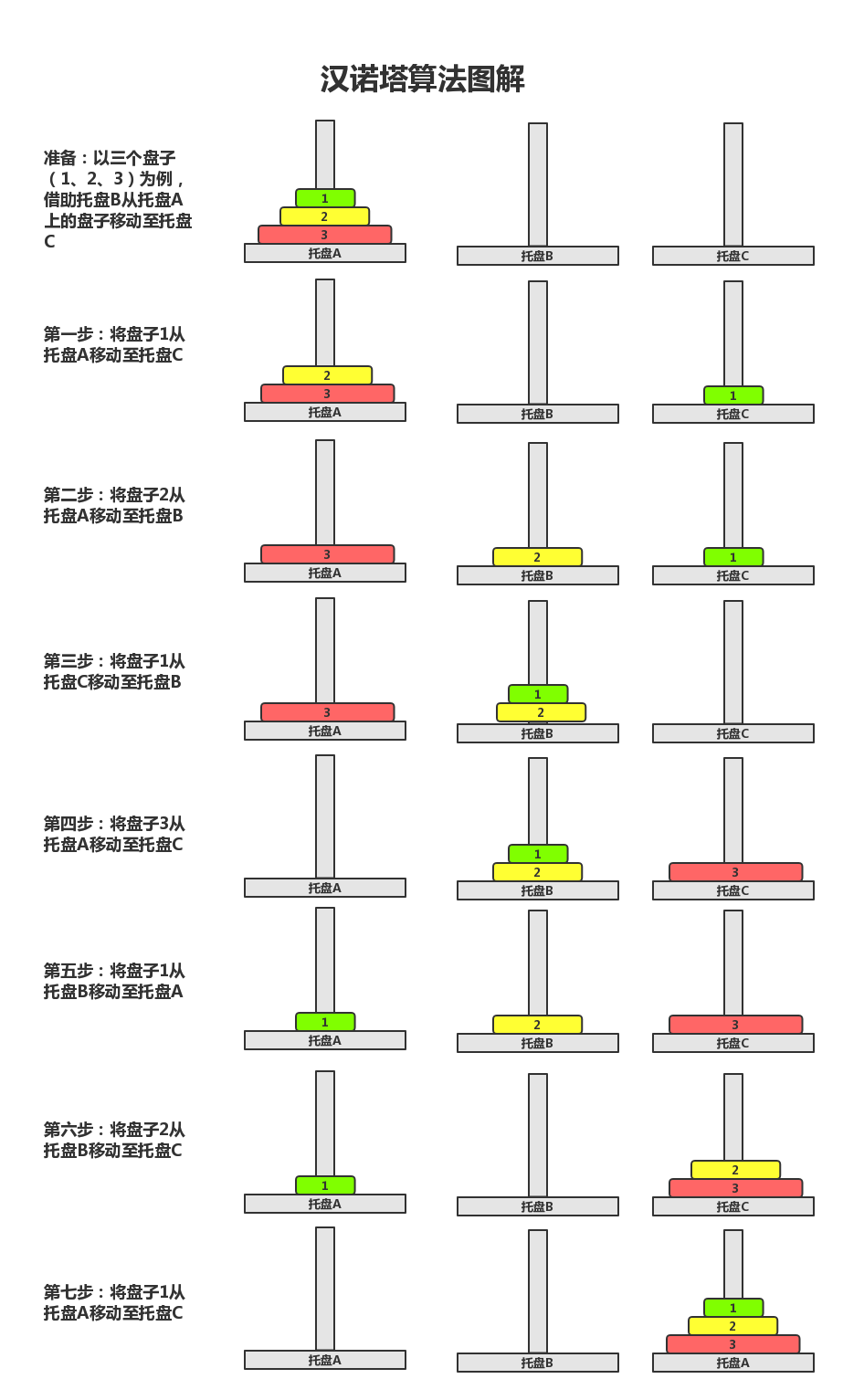
拆分成三阶汉诺塔问题解题步骤：

img20240131

图源博客：https://blog.csdn.net/weixin_45706856/article/details/131802164

通过图解我们可以知道三层汉诺塔问题的解决办法，其实我们可以假设只有两层汉诺塔，一层是第n层，将1~n-1的所有看成一层，简化成两层汉诺塔问题。

首先考虑递归终止条件：当只有一个盘子时，我们只需要将它直接从A柱子移动到C柱子即可。

当有两个或以上的盘子时，我们可以采取以下策略：

  1. 将前 n-1 个盘子从A柱子移动到B柱子（借助C柱子）；
  2. 将第n个盘子从A柱子移动到C柱子；
  3. 将B柱子上的 n-1 个盘子移动到C柱子（借助A柱子）。

这个过程可以递归进行，直到只剩下一个盘子为止。每次递归都是对n-1个盘子进行操作，因此最终可以将所有盘子从A柱子移动到C柱子。

算法应采用分治的思想，利用递归的方式，完成n层汉诺塔的移动。

圆盘移动次数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>

void hanoi(int n, char A, char B, char C) {
    if (n == 1) {
        printf("%c -> %c\n", A, C);
    }
    else {
        hanoi(n - 1, A, C, B);
        printf("%c -> %c\n", A, C);
        hanoi(n - 1, B, A, C);
    }
}

int main() {
    int n = 0;
    scanf("%d", &n);
    hanoi(n, 'A', 'B', 'C');
    return 0;
}

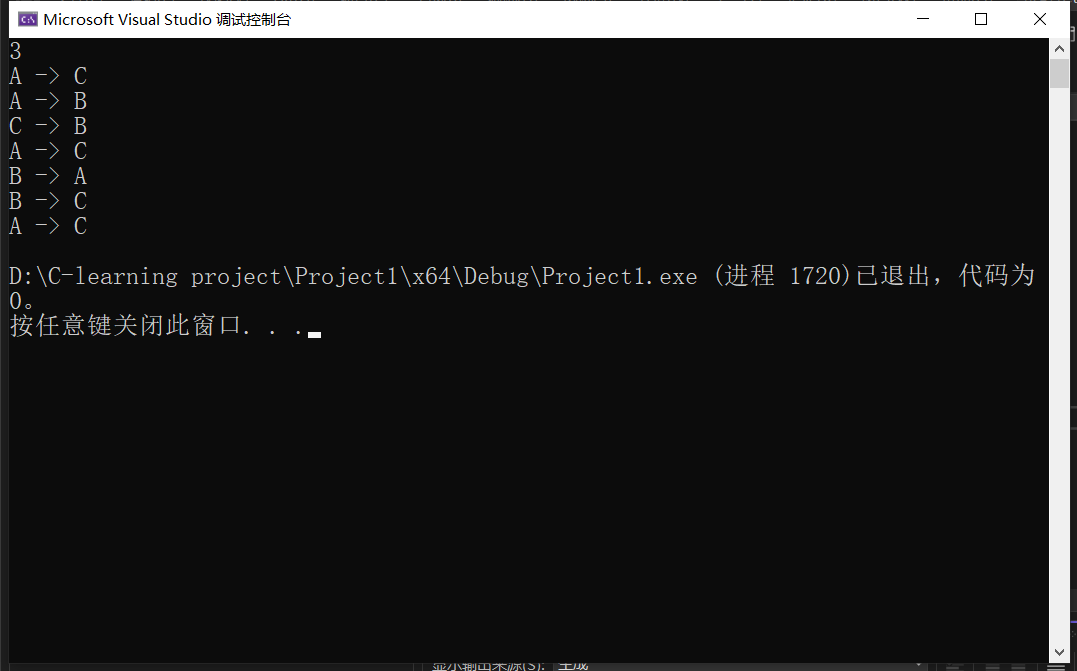
我们定义了一个名为hanoi的函数来解决汉诺塔问题，该函数接受四个参数：盘子数量n和三根柱子的名称A、B、C。

如果当前只有一个盘子，则直接将其从A柱子移动到C柱子，并输出移动方式；否则，我们将前n-1个盘子从A柱子移动到B柱子（借助C柱子），再将第n个盘子从A柱子移动到C柱子，最后将B柱子上的n-1个盘子移动到C柱子（借助A柱子）。这个过程可以递归进行，直到只剩下一个盘子为止。

在A->B中明显涉及到了复杂问题拆分，即将1到n-1看成一个盘子，所以需要第一个递归,涉及到的是在B->A时,也将当时的1到n-1看成一个盘子，进行第二次递归。

image-20240201095111466

每次递归调用hanoi函数时，传递的参数A、B、C代表了不同的柱子。

在每一次递归调用中，我们通过改变参数的顺序来实现从一个柱子到另一个柱子的移动。具体而言，A代表源柱子（初始位置），B代表辅助柱子（借助的柱子），C代表目标柱子（目标位置）。

在第一次递归调用中，我们将前 n-1 个盘子从源柱子 A 移动到辅助柱子 B（借助目标柱子 C）。然后，我们将第 n 个盘子从源柱子 A 移动到目标柱子 C。最后，在第二次递归调用中，我们将辅助柱子 B 上的 n-1 个盘子移动到目标柱子 C（借助源柱子 A）。

通过不断改变参数的顺序，我们可以确保每次递归调用都是从不同的柱子进行移动。这样，最终就能够将所有的盘子从源柱子移动到目标柱子，同时遵守汉诺塔问题的规则。

2.青蛙跳台阶问题

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个 n级的台阶总共有多少种跳法(先后次序不同算不同的结果)

假设，只有1级台阶的时候，此时青蛙只有一种跳法。

假设，此时2级台阶的时候，青蛙有两种跳法，可以选择一级一级跳，也可以选择一下子跳两级。

假设，此时3级台阶的时候，青蛙最初还是有两种跳法，可以选择初始只跳1级，也可以选择初始跳2级。当选择只跳1级时，接下来还有两级的台阶，青蛙还有两种选择，可以选择一级一级跳，也可以选择一下子跳两极，而选择初始跳2级的时候，就只能再跳1级了。

此时我们可以发现，当青蛙选择初始跳1级的时候，后续的问题又拆分成只有2级台阶的问题了，我们是不是可以用递归的思想不断拆分问题呢？

当台阶数为0或1时，青蛙只有一种跳法：不跳或者直接跳到顶层。对于其他的n，青蛙可以选择跳上一级台阶后再跳，或者跳上两级台阶后再跳。因此，青蛙跳上n级台阶的跳法数量等于跳上n-1级台阶的跳法数量加上跳上n-2级台阶的跳法数量。

有点类似斐波那契数，我们不断从前往后递归计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>

int turtleJump(int n) {
    if (n == 0 || n == 1) {
        return 1;
    }
    else {
        return turtleJump(n - 1) + turtleJump(n - 2);
    }
}

int main() {
    int n = 0;
    scanf("%d", &n);
    int result = turtleJump(n);
    printf("青蛙跳上%d级台阶的跳法数量为：%d\n", n, result);
    return 0;
}

image-20240201100749376